Tema
I quadrati magici tra matematica ed esoterismo
Quando si parla di “quadrato magico”
si intende generalmente una struttura
a forma di scacchiera con un numero
variabile di caselle. Al loro interno
vengono disposti dei numeri interi in
modo da ottenere per ogni fila orizzontale,
verticale e diagonale sempre
la medesima somma. Tale numero
viene chiamato costante magica o
somma magica.
Daniele Bui – Il Dovere, Lugano (Revista massonica svizzera
giugno/luglio 2010)
Definizione
Il quadrato magico originale era un quadrato
costituito dai primi nove numeri
interi {1,2,3,4,5,6,7,8,9}, distribuiti in
modo tale che i numeri nelle tre righe,
nelle tre colonne e nelle due diagonali,
sommati, dessero come risultato 15. Per
esempio il seguente quadrato risulta
dotato di proprietà “magiche”. In effetti,
come si vede, la sommadelle righe, delle
colonne e delle diagonali dà sempre 15.
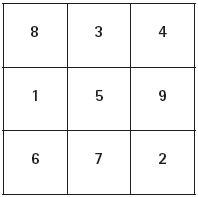

L’ordine del quadrato magico è dato dal
numero di righe o colonne. Per esempio
il quadrato appena riportato è di ordine
3 perché ha tre colonne. Un quadrato 4
x 4 viene chiamato quadrato magico di
“ordine 4”, uno 5 x 5 di “ordine 5” e così
via. In generale, un quadrato n x n (=n2)
è noto sotto il nome di quadrato di
“ordine n”. Uno dei modi più usati per
trovare lacostante magica è il seguente:
si prende l’ordine del quadrato magico,
n, e si trova il valore di½(n(n2+1), dove
il quadrato magico è formato dai numeri
naturali 1, 2, 3…,n2. In effetti ½
(3(32+1))=15. Non è stato ancora trovato
un metodo generale per costruire
un quadrato magico di ordine pari di
qualsiasi dimensione. Ci sono invece
diversi metodi generali, sui quali non
possiamo evidentemente soffermarci in
questa sede, che si possono usare per
costruire un quadrato magico di ordine
dispari di qualsiasi dimensione.
Storia
Il primo quadrato magico di cui si abbia
conoscenza è antichissimo; gli studiosi
lo collocano nell’antica Cina, ai tempi
della dinastia Shang, due millenni
prima dell’era cristiana. La leggenda
racconta di un pescatore che un giorno
lungo le rive del fiume Lo, un affluente
del fiume Giallo, vide una tartaruga che
lasciava intravedere sul guscio un
sistema di segni particolare. Dopo aver
portato la strana tartaruga dall’imperatore,
i matematici al suo servizio si
impegnarono a cercare di decifrare un
eventuale codice di tale sistema di
segni. Essi scoprirono che raffigurava
una struttura geometrica, in particolare
un quadrato di una serie di numeri che
davano come somma costante di ogni
riga, colonna e diagonale il numero 15.
Questo strano quadrato dalle proprietà
“magiche” venne chiamato Lo Shu e
assunse un valore simbolico e sacro
della Cina di quel periodo rinviando a
leggi misteriose dell’essenza dell’universo
e della matematica. Il più antico
documento che fa stato di questa leggenda
della tartaruga, senza peraltro
menzionare il tema del quadrato
magico, risale al VII secolo a.C. Dalla
Cina sembra che i quadrati magici si
sianopropagati in Indiaein Persiaapartire
dal X secolo. In seguito giunsero in
Europa non prima del XIV secolo. Come
e grazie a quali personaggi i quadrati
magici sono passati dalla Cina all’India,
all’Islam e poi in Europa resta per il
momento un mistero. Quello che si sa è
che i quadrati magici originari dalla
Cina erano di ordine 3. Infatti le prime
tracce di quadrati di ordine 4 sono state
ritrovate in India nel primo secolo d. C.
e quelle di ordine otto sono state localizzate
in Persia nel IX secolo d.C. e sono
verosimilmente legate al gioco degli
scacchi, apparso in India nell’VIII secolo.
I quadrati magici approdarono in
Europa relativamente tardi. Nel 1315
Emmanuel Moschopoulos, un filosofo
greco di Costantinopoli, scrisse un trattato
sui quadrati magici ispirandosi ai
lavori di Al Bunimaliberandoli dalla loro
sovrastruttura esoterica. Nel Rinascimento,
Luca Pacioli (1445-1517), a partire
dall’opera di Moschopoulos, costruì
un numero di quadrati di diverso ordine
epubblicò nel 1494 un libro di referenza
in matematica (Somma de Arithmetica,
Geometria, Proportioni et Proportionalità).
L’interesse esoterico riprese vigore
soprattutto con Marsilio Ficino (1493-1499) che sostenne che i quadrati
magici discendevano da documenti
cabalistici risalenti alla tarda antichità.
La tradizione esoterica si è costantemente
alimentata alle suggestioni emanate
dai quadrati magici. In questo
ambito c’è senz’altro da segnalare
l’enigmatica incisione che il pittore
Albrecht Dürer (1471-1528) creò dandole
il titolo di ”Melancolia”.

Come si vede si tratta di un quadrato
magico di ordine 4 che comprende i
primi 16 numeri. La sua costante vale
34. Il quadrato ha numerose proprietà
“magiche”. Oltre ad apparire in ogni
riga, colonna e diagonale, la costante
del quadrato magico appare anche:
- nella somma delle cifre poste ai 4
angoli (16 + 13 + 4 + 1 = 34)
- nella sommadelle quattrocifre al centro
(10 + 11 + 6 + 7= 34)
- nella somma delle cifre 15 e 14 nella
fila in basso e delle cifre 3 e 2 a loro
opposte nella fila in alto (15 + 14 + 3
+ 2= 34)
- nella somma delle cifre 12 e 8 nella
colonna di desta e delle cifre 9 e 5
poste di fronte nella colonna di
sinistra (12 + 8 + 9 + 5 = 34)
- nella somma delle cifre di ognuno dei
quattro quadrati negli angoli (16 + 3
+ 5 +10 = 34; 2 + 3 + 11 + 8 = 34; 9
+ 6 + 4 +15 = 34; 7 + 12 + 14 +1 =
34).
Spesso i quadrati magici si supponevano
dotati di virtù soprannaturali perché
rappresentavano la struttura nascosta
del cosmo, le leggi che governano
armonicamente l’universo
e quindi in ultima analisi
la ragione divina. Venivano
incisi su piastre d’oro o d’argento
ed erano consigliati
come talismani capaci di preservare
da malattie, povertà,
problemi sentimentali…
Nel contesto della tradizione
esoterica il piùcelebre ed enigmatico
quadrato magico è
senz’altro quello del “sator”.
Esso è costituito dalla
seguente struttura letterale:
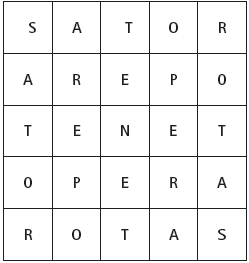
Questo quadrato rivela immediatamente
una struttura palindroma
che consente di leggere in molte direzioni
diverse la sequenza di cinque
parole, di cinque lettere ciascuna: SATOR
AREPO TENET OPERA ROTAS. Il quadrato
in questione è stato ritrovato in diversi
testi antichi ed è raffigurato su antichi
monumenti in molti luoghi europei.
Sulla sua origine e sul suo significato
sono state formulate svariate congetture.
In un primo tempo il quadrato
venne considerato un’invenzione
medievale; tutte le fonti conosciute in
effetti non erano anteriori al VI secolo.
Nel 1868, tuttavia, venne ritrovato un
graffito raffigurante il quadrato tra le
rovine di Cirencester (l’antica Corinium),
ed esso fu datato tra il II ed il IV secolo
d. C. Una delle prime ipotesi avanzate fu
quella che vedeva nel quadrato una
croce nascosta, e più precisamente
un sistema dei primi cristiani per
rappresentare la croce in forma
criptata. Infatti come osservò il
pastore evangelista Felix Grosser
nel 1926 le venticinque lettere del
quadrato possono essere disposte in
modo da formare le parole PATERNOSTER
incrociate, fra unaAeduna
O, corrispondenti alle lettere greche
alfa e omega, cioè i simboli del principio
e della fine di tutte le cose.
“Qualche difficoltà sorse per interpretare
il significato della parola
AREPO, che non esiste nella lingua
latina. Lo studioso Giuseppe Aldo Rossi
scoprì che nelle Gallie esisteva un’unità
di misura di superficie che veniva chiamata
semiiugerum o arepennis.
Quest'ultima parola sembrava derivare
dal nome del carro arepos, utilizzato nei
lavori agricoli. Rossi ipotizzò allora che
il celtico arepos diventasse per i latini
arepus. A conferma di tale ipotesi venne
ritrovata un'edizione della Bibbia greca
del XIV secolo che, riportando una traduzione
del quadrato magico, traduceva
la parolaAREPO con laparolagreca arotron
che significa carro. Utilizzando tale
ipotesi le parole del quadrato vennero
interpretate nel modo seguente: «Il
Seminatore, col suo carro, tiene con
cura le ruote». Altri autori hanno proposto diverse interpretazioni. Ad esempio,
Ludwig Diehl, fornì la seguente traduzione:
«Il seminatore possiede le opere»,
ovvero «Dio è il Signore del creato». In
ogni caso vi fu un sostanziale accordo
nel ritenere che il quadrato avesse un
significato cristiano e che la sua origine
fosse collocabile in Gallia e databile
intorno al III secolo d.C.” (Fuso, 2006,
p.180)

Tuttavia, nel 1925 e nel 1936, due
esemplari del quadrato vennero ritrovati
negli scavi archeologici di Pompei.
Tale scoperta costituì verosimilmente
una confutazione dell’ lnterpretazione
che ipotizzava un’origine cristiana del
quadrato. Anche in altre parti d’ Europa
si trovano esemplari di questo quadrato.
Per esempio “in Francia nella chiesa san
Lorenzo di Rochemaure; in una vecchia
abitazione di Le-Puy; nei castelli di Chinon,
di Jarnac e di Gisors. In Spagna a
san Giacomo di Compostela, in Ungheria
in una villa romana di Acquincum,
l’odierna Altofen” (Ibid.) Alla luce del
fatto che alcune tra queste località
furono possedimenti dei templari,
diversi studiosi hanno supposto un
legame fra il quadrato magico e il celebre
ordine religioso-militare. Altri autori
hanno inoltre formulato interpretazioni
esoteriche, cabalistiche e astrologiche
del quadrato magico. Davanti ad una
serie di interpretazione pur coerenti ma
incompatibili resta a tutt’oggi azzardato
pronunciarsi con certezza sull’origine
e sul significato del quadrato del
“sator”.
Massoneria
Le suggestioni simboliche inerenti ai
quadrati magici hanno fornito elementi
da interpretare anche in chiave massonica.
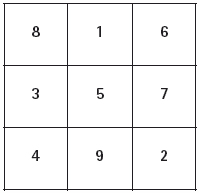
Oswald Wirth per esempio, nel suo
Libro del maestro, facendo riferimento
al seguente quadrato magico di saturno
(cioè di ordine 3) assimila le cifre della
prima colonna (8-3-4) alla colonna J del
tempio, quelli della terza colonna alla
colonna B, 1, 5 e 9 che si rapportano
rispettivamente all’Apprendista, al
Compagno e al Maestro piazzati tra le
colonne. L’Apprendista deve prima di
tutto distinguere 8 (ragione e rigore) da
6 (sentimento e bontà). Il Compagno
deve distinguere 3 (concezione teorica
e astratta) e 7 (esecuzione pratica e
concreta). Il maestro 4 (positivismo
matematico) e 2 (sottili capacità intuitive).
In diagonale si oppongono anche
2 (lo sconosciuto e l’inesplorato) e 8
(logica, ordine, legge), 4 (volere positivo
che ordina) e 6 (aspirazione sentimentale).
L’iniziazione parte da 8 (ragionamento
dell’Apprendista esercitato nei
limiti del compasso) per approdare a 2
(veggenzadel maestroche sonda le profondità
dell’infinito). Come sottolinea
Jean-claude Michaud (cfr. capitolo IV) il
quadrato magico è simile allo specchio
della regina nella fiaba di Biancaneve:
risponde alle questioni che gli si pone.
Possiede un’architettura suscettibile di
accogliere questioni di ordine metafisico,
cosmologico, spirituale, esistenziale
a dipendenza della particolare
inclinazione dell’animo di chi lo interroga.
I riflessi dello specchio, e quindi
del quadrato, sono le risposte indirette
alle nostre domande fondamentali svelate
dalla nostra anima profonda. Lo
specchio non può mentire se il soggetto
che pone le domande è sincero con sé
stesso. Come la superficie immobile
dell’acqua limpida e pura il quadrato
magico lascia anch’esso trasparire l’immagine
oggettiva della realtà, in tal
senso rappresenta sempre e in primo
luogo una preziosa fonte di autentica
verità.
Interessi matematici
Diversi matematici hanno lasciato un
contributo significativo allo studio dei
quadrati magici. Per quanto riguarda
l’Asia, un matematico cinese del XIII
secolo, Yang Hui formulò il primo algoritmo
di costruzione dei quadrati magici
di ordine 4. Sviluppi interessanti nello
studio dei quadrati magici avvennero in
Giappone all’inizio del periodo Edo
(1603-1867). In particolare due matematici,
Seki Takakazu (1642-1708) e
Tanaka Yioshizane (1651-1719) costruirono
dei quadrati concentrici di ordine
7,8,9 e 10 che stupiscono ancora oggi.
In Europa, specialmente in Francia, i
quadrati magici polarizzarono l’interesse
di matematici e filosofi di primo
ordine. Pierre de Fermat (1601-1665)
costruì il primo cubo di ordine 4. Blaise
Pascal (1623-1662) scrisse in seguito un
trattato sui quadrati magici, il Traité des
nombres magiquement magiques, che
indirizzò all’Accademia delle scienze nel
1654. Tra gli intellettuali francesi del
XVII secolo che si sono interessati ai
quadrati magici non bisogna dimenticare
il padre Marin Mersenne (1588-
1648), amico di Fermat, a cui dobbiamo
differenti memorie sulla teoria dei
numeri o Bernard Fénicle de Bessy
(1605-1675), un corrispondente di
Mersenne, che fu il primo a pubblicare
una lista di 880 quadrati di ordine 4. Nel
XVIII secolo il grande matematico Leonhard
Euler (1707-1783) studiò i quadrati
magici e ne schizzò la teoria in
un’opera intitolata De Quadratis Magicis,
apparso nel 1776. Anche Benjamin
Franklin (1706-1790) si interessò ai
quadrati magici e ne divenne un abile
costruttore. L’interesse per i quadrati
magici restò vivo anche nel XIX secolo.
Numerosi sono i matematici che cercarono
di mettere a punto un metodo per
la loro costruzione. Ci provò anche il
grande Friedrich Gauss (1777-1855),
tuttavia, come detto, nessuno riuscì a
scoprire un metodo di costruzione
generale: gli algoritmi sono differenti a
dipendenza dell’ordine pari o dispari dei
quadrati. Con l’avvento dei calcolatori elettronici, nella seconda metà del XX
secolo, e i recenti sviluppi dell’informatica
la costruzione dei quadrati magici
èdiventata piùsemplice ed ha permesso
l’ideazione di altre strutture geometriche
“magiche” come stelle, cerchi, cubi
e ipercubi, cioè enti geometrici che
sembrano persino aprire itinerari di
ricerca inediti negli studi matematici.
Conclusioni
È piuttosto curioso, e anche paradossale,
che i quadrati magici possano
essere stati oggetto di interesse parallelo
tra i cultori di scienze occulte o
esoteriche e di alcuni tra i più grandi
scienziati. In realtà la stessa rivoluzione
scientifica del XVI e XVII secolo,
come la recente e più aggiornata storiografia
ha messo in rilievo con
abbondanza di dati, manifesta una
rilevante presenza della tradizione
magica e di quella ermetica all’interno
del processo che è la rivoluzione scientifica.
In altri termini si può dire che la
scienza moderna pubblica nei controlli,
assoggettata ad un metodo
rigoroso ed oggettivo, con le sue istituzioni
e con il suo linguaggio univoco
e chiaro è il risultato di un lungo processo
in cui si intrecciano misticismo,
ermetismo, magia, alchimia e astrologia.
Quel Rinascimento che abitualmente
viene presentato come l’età del
rinnovamento delle arti e dell’emergenza
del sapere scientifico è anche il
tempo della magia per eccellenza. Un
tempo che proietta la sua ombra persino
sulla nostra epoca, in apparenza
razionale e disincantata, ma che si
interessa ancora a miracoli ed oroscopi,
filtri d’amore e fatture più o
meno maligne. Se può suscitare un
certo stupore l’interesse convergente
verso i quadrati magici dei cultori di
discipline occulte e degli addetti alla
scienza propriamente detta, ancora
più stupefacente ci sembra l’interesse
costante che questi poligoni, apparentemente
di scarsa importanza e probabilmente
inutili da un punto di vista
economico e militare, hanno saputo
esercitare di generazione in generazione
passando indenni attraverso i
secoli e scavalcando con una facilità
sconcertante culture, popoli e lingue
dell’intero pianeta. Tra le diverse proprietà
“magiche” di questi quadrati
annovererei quindi pure l’inossidabilità
ai cambiamenti epocali di tempo,
ma anche di spazio, che queste particolari
griglie numeriche hanno saputo
dimostrare .
|
 |